Question

Please help :c

the first word is find

Answer 1

The values of
`r_(2)` and
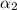`\alpha_(2)` are 2 and 150º.

Explanation:

The complete statement is:

Find
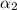`\alpha_(2)` and
`r_(2)` such that
`\sin \theta - √(3)\cdot \cos \theta = r_(2)\cdot \cos (\theta - \alpha_(2))`.

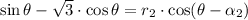We proceed to use the following trigonometric identity:

`\cos (\theta - \alpha_(2)) = \cos \theta \cdot \cos \alpha_(2) +\sin \theta \cdot \sin \alpha_(2)` (1)

`\sin \theta -√(3)\cdot \cos \theta = r_(2)\cdot \cos \theta \cdot \cos \alpha_(2)+r_(2)\cdot \sin \theta \cdot \sin \alpha_(2)`

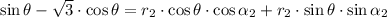
By direct comparison we derive these expressions:

`r_(2)\cdot \sin \alpha_(2) = 1` (2)

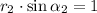`r_(2)\cdot \cos \alpha_(2) 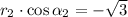= -√(3)` (3)

By dividing (2) by (3), we have the following formula:

`\tan \alpha_(2) = -(1)/(√(3))`

`\tan \alpha_(2) = -(√(3))/(3)`

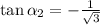
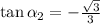
The tangent function is negative at second and fourth quadrants. That is:

`\alpha_(2) = \tan^(-1) \left(-(√(3))/(3) \right)`

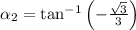
There are at least two solutions:

`\alpha_(2,1) = 150^(\circ)`,
`\alpha_(2,2) = 330^(\circ)`

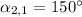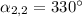
And the value of
`r_(2)`:

`r_(2)^(2)\cdot \sin^(2)\alpha_(2) + r_(2)^(2)\cdot \cos^(2)\alpha_(2) = 4`

`r_(2)^(2) = 4`

`r_(2) = 2`

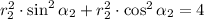
The values of
`r_(2)` and
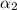`\alpha_(2)` are 2 and 150º.