Hello!
First, let's rewrite the function:
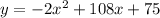
Now, let's find each coefficient of it:
• a = -2
,
• b = 108
,
• c = 75
As we have a < 0, the concavity of the parabola will face downwards.
So, it will have a maximum point.
To find this maximum point, we must obtain the coordinates of the vertex, using the formulas below:
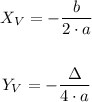
First, let's calculate the coordinate X by replacing the values of the coefficients:
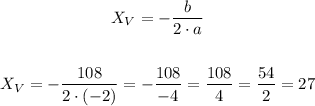
So, the coordinate x = 27.
Now, let's find the y coordinate:

The coordinate y = 1533.
Answer:
The maximum profit will be 1533 (value of y) when x = 27.