Question

In ∆ABC, m∠A = 60º, m∠C = 30º, and AB = 6 inches. What is the length of side BC?

Answer 1

ABC is a 30 60 90 triangle
In such a triangle, the shortest side AB multiplied by the square root of 3 equals the length of the "medium" side CB.
6 * sq root (3) = 10.39
(Incidentally, the hypotenuse AC = short side*2 = 12)

Answer 2

`6√(3)\approx 10.39` inches.

Explanation:

We have been given that in ∆ABC,
`m\angle A=60^(\circ)`,
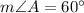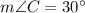`m\angle C=30^(\circ)`, and the length of segment AB is 6 inches. We are asked to find the length of side BC.

We can see from our attachment that in ∆ABC, the side BC is opposite side and side AB is the adjacent side for the angle A.

Since tangent relates the opposite side of a right triangle with hypotenuse, so we can set an equation to find the length of side BC as:

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(60^(\circ))=\frac{\text{BC}}{6}`

`√(3)=\frac{\text{BC}}{6}`

`√(3)* 6=\frac{\text{BC}}{6}* 6`

`6√(3)=\text{BC}`

`\text{BC}\approx 10.39`

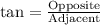
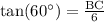
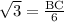
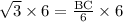
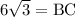
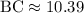
Therefore, the length of side BC is
`6√(3)\approx 10.39` inches.