Question

A painting is worth $9000 in 2007. The value of the painting increases by 12% eachyear.Estimate the length of time it takes for the value of the painting to double.

Answer 1

Step 1

State the formula for exponential growth

`P(0)=P(1+r)^t`

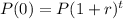
where;

`\begin{gathered} P=\text{ worth in 2007=\$9000} \\ r=rate=(12)/(100)=0.12 \\ t=\text{ time for growth in years} \\ P(0)=\text{ Required value of growth in t years} \end{gathered}`

Step 2

Find double the value of the painting.

`2P=9000*2=\text{ \$18000}`

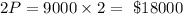
Step 3

Estimate the length of time it takes for the value of the paint to double

`\begin{gathered} 18000=9000(1+0.12)^t \\ (18000)/(9000)==(9000(1+0.12)^t)/(9000) \\ 2=(1+0.12)^t \end{gathered}`
`\begin{gathered} \ln 2=\ln (1.12)^t \\ \ln 2=t\ln (1.12) \\ (t(\ln1.12))/(\ln1.12)=(\ln2)/(\ln1.12) \\ t=6.116255374\text{ years} \\ t\approx6.1163years\text{ approxi}mately\text{ to 4 decimal places} \end{gathered}`

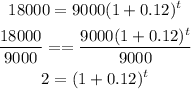
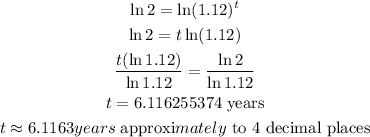
Hence, it will take approximately 6.1163 years for the value of the paint to double.