Answer:
C) 0.739
Explanation:
We have been given Uranium-233 is decaying at a constant 57% rate per day. There were 3,820 pounds of Uranium-233 produced from a power plant.
To find the amount of uranium left after 15 days we will use continuous exponential decay function.
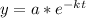 , where,
, where,
a = Initial amount,
e = Mathematical constant,
k = A number representing decay rate in decimal form.
t = Time.
Let us convert our given rate in decimal form.
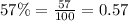
Upon substituting our given values in above formula we will get,
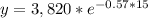
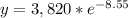
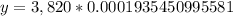
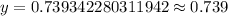
Therefore, the amount of Uranium-233 after 15 days will be 0.739 pounds and option C is the correct choice.