Answer: B.) 85,688
Explanation:
The exponential decay equation is given by :-
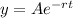 , where A is the initial amount , r is the rate of decay and t is time period.
, where A is the initial amount , r is the rate of decay and t is time period.
Given : Rate of decay for every hour:
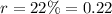
Time period :
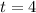
Put y = 35,542 , r = 0.22 and t=4 in the above equation , we get

Hence, the initial population in the city before the epidemic broke out =85,688