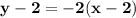Answer:
1) equation of line is: y-3=0
2) equation of line is:
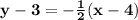
3) equation of line is:
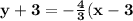
4) equation of line is:
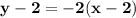
Explanation:
We need to find the equation of the line using Two-Point form.
The general equation of two-point form is:
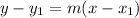 where m is slope.
where m is slope.
The formula used to calculate slope is:
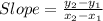
1. (1,3) and (-2,3)
First finding slope
We have:
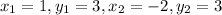
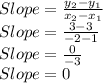
So, equation of line will be:
Using slope m=0 and point (1,3)

So, equation of line is: y-3=0
2. (4,3) and (6,2)
First finding slope
We have:
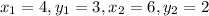
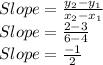
So, equation of line will be:
Using slope m=
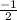 and point (4,3)
and point (4,3)
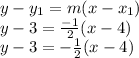
So, equation of line is:
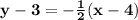
3) (3,-3) and (0,1)
First finding slope
We have:
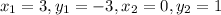
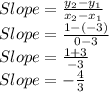
So, equation of line will be:
Using slope m=
 and point (3,-3)
and point (3,-3)
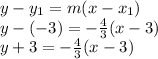
So, equation of line is:
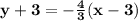
4) (2,2) and (4,-2)
First finding slope
We have:

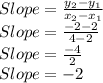
So, equation of line will be:
Using slope m=-2 and point (2,2)
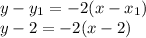
So, equation of line is: