Question

Confirm that f and g are inverses by showing that f(g(x)) = x and g(f(x)) = x. (2 points)

f of x equals eight divided by x and g of x equals eight divided by x

Answer 1

we can say that f and g are inverses of each other because f(g(x)) = x and g(f(x)) = x

Explanation:

We need to confirm that f and g are inverses by showing that f(g(x)) = x and g(f(x)) = x.

We have

`f(x)= (8)/(x)\\g(x)=(8)/(x)`

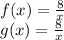
Now, finding f(g(x))

Put x = 8/x in f(x)

`f(g(x)) =(8)/((8)/(x) )\\=8/ (8)/(x)\\=8 * (x)/(8)\\=x`

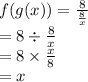
So, we get f(g(x))=x

Now, find g(f(x))

Put x = 8/x in g(x)

`g(f(x)) =(8)/((8)/(x) )\\=8/ (8)/(x)\\=8 * (x)/(8)\\=x`

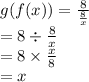
So, we get g(f(x)) = x

Therefore we can say that f and g are inverses of each other because f(g(x)) = x and g(f(x)) = x