Let

be the length of the rectangle, and let

be its width. The perimeter of a rectangle is the sum of all its side lengths:
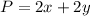
(since there are two sides of length

and two sides of length

)
You know the perimeter is 18 meters, so the equation above is
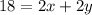
Now, you also know that the length of the rectangle is 5 meters longer than the width, which means
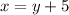
, or equivalently,
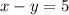
. So you have two equations depending on

and

:
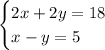
From here, you could substitute the second equation into the first to get an equation only in terms of the width

. Since
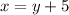
, you have
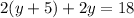
and solve for

from there (but you're not asked to do so).