
means there exists some

such that whenever

, it's guaranteed that
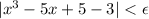
for all
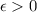
.
You have

Completing the square for the quadratic term yields
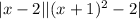
and by the triangle inequality,
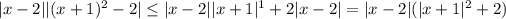
Suppose we fix
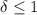
. Then if
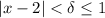
, it follows that
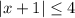
, since
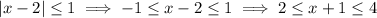
This means
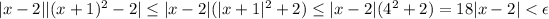
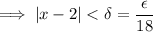
So to guarantee that
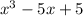
is within

of the limit, we can choose the smaller of the two choices for

, or

.
Now, when
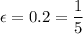
, you would have

, and when
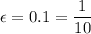
, you would have
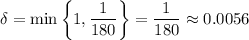
.