Question

Hard qn on Trigonometric equations and identities, please help​

Answer 1

(i)
`OE = 0.6\cdot \sin \theta + 1.4\cdot \cos \theta`, (ii)
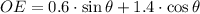`\theta \approx 33.368^(\circ)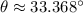`, (iii) The maximum value of OE is approximately 1.523 meters, which is associated with an angle of approximately 23.199º.

Explanation:

(i) From Geometry, we get that sum of internal angles of trangle AOD.

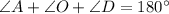`\angle A + \angle O + \angle D = 180^(\circ)` (1)

If we know that
`\angle O = 90^(\circ)` and
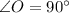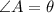`\angle A = \theta`, then the value of
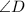`\angle D` is:

`\angle D = 180^(\circ)-90^(\circ)-\theta`

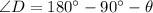
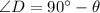`\angle D = 90^(\circ)-\theta` (2)

But we also have the following identity:

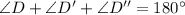`\angle D +\angle D' +\angle D'' = 180^(\circ)` (3)

If we know that
`\angle D = 90^(\circ)-\theta` and
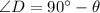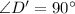`\angle D' = 90^(\circ)`, then the value of
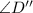`\angle D''` is:

`90^(\circ)-\theta +90^(\circ)+\angle D'' = 180^(\circ)`

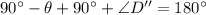
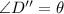`\angle D'' = \theta` (4)

By Trigonometry, we derive the following formula:

`OE = OD +DE`

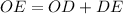
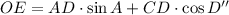`OE = AD\cdot \sin A +CD\cdot \cos D''` (5)

If we know that
`AD = 0.6\,m`,
`CD = 1.4\,m`,
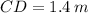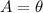`A = \theta` and
`D'' = \theta`, then the value of OE is:

`OE = 0.6\sin \theta + 1.4\cos \theta` (6)

(ii) If we know that
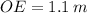`OE = 1.1\,m`, then the value of
`\theta`:

`0.6\cdot \sin \theta + 1.4\cdot \cos \theta = 1.1`

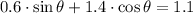
By trial and error, we find that
`\theta \approx 33.368^(\circ)`.

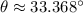(iii) Let
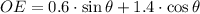`OE = 0.6\cdot \sin \theta + 1.4\cdot \cos \theta`, the first and second derivatives of the function are, respectively:

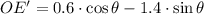`OE' = 0.6\cdot \cos \theta -1.4\cdot \sin \theta` (7)

`OE'' = -0.6\cdot \sin \theta -1.4\cdot \cos \theta` (8)

We equalize the first derivative of the function to zero and solve for
`\theta`:

`0.6\cdot \cos \theta - 1.4\cdot \sin \theta = 0`

`1.4\cdot \sin \theta = 0.6\cdot \cos \theta`

`\tan \theta = (0.6)/(1.4)`

`\theta \approx \tan^(-1) (0.6)/(1.4)`

`\theta \approx 23.199^(\circ)`

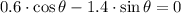
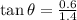
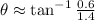
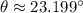
And we evaluate the second derivative:

`OE'' = -0.6\cdot \sin 23.199^(\circ)-1.4\cdot \cos 23.199^(\circ )`

`OE'' = -1.523`

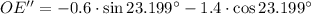
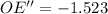
Then, the critical value is associated with an absolute maximum.

The maximum value of OE is:

`OE = 0.6\cdot \sin 23.199^(\circ)+1.4\cdot \cos 23.199^(\circ )`

`OE \approx 1.523\,m`

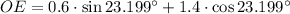
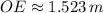
The maximum value of OE is approximately 1.523 meters, which is associated with an angle of approximately 23.199º.