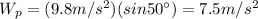Question

A box with a mass of 100.0 kg slides down a ramp with a 50 degree angle. What is the weight of the box? N What is the value of the normal force? Round the answer to the nearest whole number. N What is the acceleration of the box? (Disregard friction and air resistance.) Round the answer to the nearest tenth.

Answer 1

1) weight of the box: 980 N

The weight of the box is given by:

`W=mg`

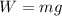
where m=100.0 kg is the mass of the box, and
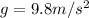`g=9.8 m/s^2` is the acceleration due to gravity. Substituting in the formula, we find

`W=(100.0 kg)(9.8 m/s^2)=980 N`

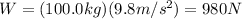
2) Normal force: 630 N

The magnitude of the normal force is equal to the component of the weight which is perpendicular to the ramp, which is given by

`N=W cos \theta`

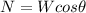
where W is the weight of the box, calculated in the previous step, and
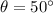`\theta=50^(\circ)` is the angle of the ramp. Substituting, we find

`N=(980 N)(cos 50^(\circ))=630 N`

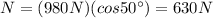
3) Acceleration:
`7.5 m/s^2`

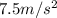
The acceleration of the box along the ramp is equal to the component of the acceleration of gravity parallel to the ramp, which is given by

`a_p = g sin \theta`

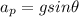
Substituting, we find

`W_p = (9.8 m/s^2)(sin 50^(\circ))=7.5 m/s^2`