Question

When doing right triangle trigonometry how do you determine which sine you use like sin, cos etc?

Answer 1

Let's draw a right triangle to guide us:

Every right triangle will have one hypotenuse side and two leg sides. The hypotenuse is always the bigger one and it is always opposite to the right angle, so in this triangle the hypotenuse is a (the letter can change from exercise to exercise, but it is always the opposite to the rignt angle).

The legs can be classified as adjancent or opposite legs, but this is with respect to the angle we are using.

So, if we are using angle C, the opposite leg is the leg that is opposite to angle C, that is, c.

Thus, the adjancent leg is the leg that is touching the angle C, that is, b.

So, with respect to angle C, we have:

Hypotenuse - a

Opposite leg - c

Adjacent leg - b

The sine is the ratio between the opposite leg and the hypotenuse, always.

The cosine is the ratio between the adjacent leg and the hypotenuse, always.

The tangent is the ratio between the opposite leg and the adjacent leg, always.

For, for angle C, we have:

`\begin{gathered} \sin C=(c)/(a) \\ \cos C=(b)/(a) \\ \tan C=(c)/(b) \end{gathered}`

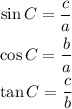
For angle B, we do the same, however now, the legs are switched, because the leg that is opposite to angle B is b and the leg that is adjance to angle B is c, so, for angle B:

Hypotenuse - a

Opposite leg - b

Adjacent leg - c

And we follow the same for sine, cosine and tangent but now for angle B and with the legs switched:

`\begin{gathered} \sin B=(b)/(a) \\ \cos B=(c)/(a) \\ \tan B=(b)/(c) \end{gathered}`

Questions regaring these ratios normally will present 2 values and ask for a third value. One of the values will be an angle, the other will be side (usually). So, we need to identify which angle are we working with and which sides are the hypotenuse, the opposite leg and adjancent leg with respect to the angle we will work with. Then we identify which of the side we will use and pick the ratio thet relates the sides we will use.