Question

The circle has center O. Its radius is 4 cm, and the central angle a measures 30°. What is the area of the shaded region?Give the exact answer in terms of pi, and be sure to include the correct unit in your answer

Answer 1

Step-by-step explanation

The area of a portion of a circle with radius 'r' and central angle 'a' in radians is:

`A_{\text{portion}}=(1)/(2)\cdot r^2\cdot a`

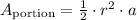
In this problem, the radius is r = 4cm, and the angle a = 30º.

First we have to express the angle in radians:

`a=30º\cdot(\pi)/(180º)=(1)/(6)\pi`

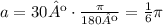
And now we can find the area of the shaded region:

Answer

The area of the shaded region is:

`A=(4)/(3)\pi cm^(2)`