Answer: B. 16.72 years
Explanation:
If interest is compounded bi-monthly, the formula to calculate the accumulated amount (A) is given by:-
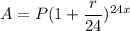 , where P = principal , r= rate of interest, x= time period(years).
, where P = principal , r= rate of interest, x= time period(years).
[1 year =12 months, total periods in 12 months if period per month is 2 = 2 x 12 =24]
Given: P= 1000, A= 2000, r= 4.15% = 0.0415
Substitute all values in formula , we get
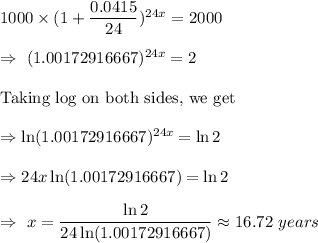
Hence, option B. is correct.