Question

If an object is dropped from a height of 55 feet, the function d=-16t^2+55 gives the height of the object after t seconds. Graph this function. Approximately how long does it take the object to reach the ground (d=0)?

Answer 1

to find the time to reach ground solve -16t^2 +55 = 0

t^2 = 55/16
t = sqrt55 / 4 = 1.85 seconds

Answer 2

Approximately 1.85 sec does it take the object to reach the ground

Explanation:

As per the statement:

If an object is dropped from a height of 55 feet

⇒
`h_0 = 55` ft

The function is given by:

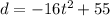`d = -16t^2+55` .....[1] gives the height of the object after t seconds.

We make the table for some values of t.

t d

0 55

1 39

2 -9

3 -89

4 -201

Plot these points on the coordinate plane.

You can see the graph as shown below.

Now, find how long does it take the object to reach the ground (d=0).

Substitute d = 0 in [1] we have;

`0 = -16t^2+55`

⇒
`16t^2 = 55`

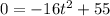
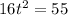
Divide both sides by 16 we get;

`t^2 = 3.4375`

⇒

`t =\pm √(3.4375)`

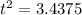
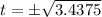
Since, t cannot be in negative.

⇒
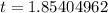`t = 1.85404962` second.

Therefore, Approximately 1.85 sec does it take the object to reach the ground