Question

A polynomial equation with rational coefficients has the roots:​

Answer 1

Answer: (5 - √1) and (4 + √7)

Explanation:

Here we have 4 roots, then this is a polynomial of 4th degree.

We can write it as

a*x⁴ + b*x³ + c*x² + d*x + e = 0

We could rewrite this as the product of two quadratic equations:

(a₁*x² + b₁*x + c₁)*(a₂*x² + b₂*x + c₂) = 0

This will be equal to zero when (a₁*x² + b₁*x + c₁) is equal to zero, and when

(a₂*x² + b₂*x + c₂) is equal to zero.

Then we need to find the roots of these two quadratic equations.

And we know that the roots of a quadratic equation like:

a₁*x² + b₁*x + c₁ are given by:

`x = (-b +- √(b^2 - 4*a*c) )/(2*a) = (-b)/(2a) +-(√(b^2 - 4ac))/(2a)`

Then the general form of the roots is something like:

`A +-√(B)`

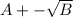
This means that if one of the roots is:

5 + √1, we must have another root equal to 5 - √1

And if we have one root equal to 4 - √7, then we must have another root equal to 4 + √7

Then the correct options are:

(5 - √1) and (4 + √7)