Given:
The results of the simulation.
Number of puppies = 4
To find:
The estimated probability that at least two of the puppies will be female.
Solution:
Let heads (H) = Female puppy.
Let tails (T) = Male puppy.
The results of the simulation are HHHH, TTTH, TTHH, HHTT, THTH, HTTH, HHHT, HHTT, HTHH, THTT.
Total outcomes = 10
The results having 2 or more H are HHHH, TTHH, HHTT, THTH, HTTH, HHHT, HHTT, HTHH.
Favorable outcomes = 8
Now,
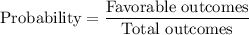
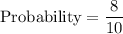
Probability in % is

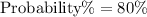
The estimated probability that at least two of the puppies will be female is
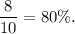
Therefore, the correct option is B.