Question

Find apolynomial function of degree3 f(10)=17,and thezeros are 0,5 and8

Answer 1

Given:

Degree of a polynomial = 3

Zeros of the polynomial = 0,5,8

f(10)=17

To find:

The polynomial function.

Solution:

The general form of a polynomial is

`P(x)=a(x-c_1)^(m_1)(x-c_2)^(m_2)...(x-c_n)^(m_n)`

Where, a is a constant,
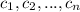`c_1,c_2,...,c_n` are zeros with multiplicity
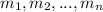`m_1,m_2,...,m_n` respectively.

Since, 0,5,8 are zeros of the polynomial, therefore, (x-0),(x-5), (x-8) are the factors of required polynomial.

`f(x)=a(x)(x-5)(x-8)` ...(i)

Putting x=10, we get

`f(10)=a(10)(10-5)(10-8)`

We have f(10)=17.

`17=a(10)(5)(2)`

`17=a(100)`

`(17)/(100)=a`

`0.17=a`

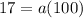
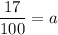
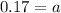
Putting a=0.17 in (i).

`f(x)=0.17(x)(x-5)(x-8)`

Therefore, the required polynomial is
`f(x)=0.17(x)(x-5)(x-8)`.