Question

What is the measure or ENV

Answer 1

first we need to get x
<RNA = <ENV [v.o.a]
8x+12=5x+57
8x-5x=57-12
3x=45
x=15

<ENV= (5×15+57)
<ENV =132
the answer is D

Answer 2

Answer: The answer is (D)
`132^\circ.`

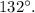
Step-by-step explanation: We are given a figure where the line segments AE and RV are intersecting at the point N. We are to find the measure of
`\angle ENV.`

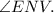
Also, given that

`\angle ANR=(8x+12)^\circ,\\\\\angle ENV=(5x+57)^\circ.`

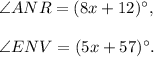
Since the line segments AE and RV intersect at N, so we have

`\angle ANR=\angleENV~[\textup{vertically opposite angles}]\\\\5x+57=8x+12\\\\\Rightarrow8x-5x=57-12\\\\\Rightarrow3x=45\\\\\Rightarrow x=15.`

Therefore,

`\angle ENV=(5* 15+57)^\circ=(75+57)^\circ=132^\circ.`

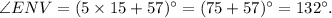
Thus, (D) is the correct option.