Question

A medical scientist has a 15-gram sample of I-13, And would like to know it's half-life in days. he also knows that k=0.0856

find the half-life, in days, of I-131 using the information at the left. round to the nearest tenth

Answer 1

8.1

Explanation:

Answer 2

The number of days is approximately 8.

Explanation:

Given : A medical scientist has a 15-gram sample of I-13, And would like to know it's half-life in days. he also knows that k=0.0856.

To find : The half-life, in days, of I-131 using the information at the left?

Solution :

The decay model is given by
`N=N_0e^(-Kt)`

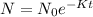
We have given that,

The substance's half-life is the time it takes for the substance to decay to half its original amount.

i.e.
`N=(N_0)/(2)`

The value of k is k=0.0856.

Substitute the values in the formula,

`N=N_0e^(-Kt)`

`(N_0)/(2)=N_0e^(-(0.0856)t)`

`(1)/(2)=e^(-(0.0856)t)`

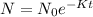
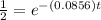
Taking natural log both side,

`\ln(1)/(2)=\ln e^(-(0.0856)t)`

`-\ln2=-(0.0856)t\ln e`

`t=(-\ln2)/(-0.0856)`

`t=8.09`

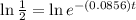
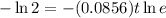
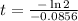
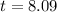
Therefore, The number of days is approximately 8.