Answer:
The correct option is B
Explanation:
Given information: ∠F=32°,∠D=54° and DF=18m.
According to the angle sum property of triangle, the sum interior angles of a triangle is 180°.
Using angle sum property, we get
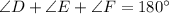
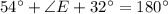
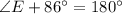
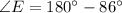
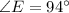
Law of sine:

Using law of sine we get
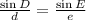
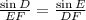
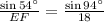
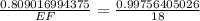
Cross multiply,
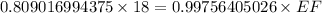
Divide both sides by 0.99756405026.
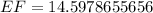
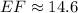
The value of EF is 14.6 m. Therefore the correct option is B.