Question

Find all values of x at which the tangent line to the given curve satisfies the stated property y=xsquared +1 over x+1; parallel to the line y = x the answer is supposed to be none

Answer 1

`y=(x^2+1)/(x+1)\implies y'=(2x(x+1)-(x^2+1))/((x+1)^2)=(x^2+2x-1)/((x+1)^2)`

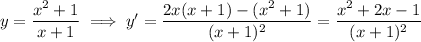
Any line parallel to
`y=x` will have the same slope of 1, so you're looking for all
`x` such that
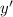
`y'` above also evaluates to 1.


`(x^2+2x-1)/((x+1)^2)=1\implies x^2+2x-1=(x+1)^2`

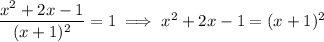
This assumes
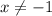
`x\\eq-1`, which is of course the case because
`x=-1` lies outside the function's domain.


`x^2+2x-1=x^2+2x+1\implies -1=1`

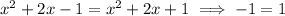
which is not true. This means no tangent line to
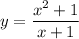
`y=(x^2+1)/(x+1)` will ever be parallel to
`y=x`.