Question

Determine whether the series is absolutely convergent 1-(1*3/3! (1*3*5/5!-（3*5*7）

Answer 1

It's not clear what your series is, so I'm going to take a wild guess on what it is you mean:


`1-(1*3)/(3!)+(1*3*5)/(5!)-(1*3*5*7)/(7!)+\cdots`

`=\displaystyle\sum_(n=1)^\infty((-1)^(n-1))/((2n-1)!)\prod_(k=1)^n(2k-1)`

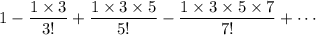
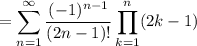
For the sum to be absolute convergent, the sum of the absolute value of the summand must converge, so you are really examining the convergence of


`\displaystyle\sum_(n=1)^\infty\frac1{(2n-1)!}\prod_(k=1)^n(2k-1)`

This is easily checked with the ratio test:


`\displaystyle\lim_(n\to\infty)\left|\frac{\displaystyle\frac1{(2(n+1)-1)!}\prod_(k=1)^(n+1)(2k-1)}{\displaystyle\frac1{(2n-1)!}\prod_(k=1)^n(2k-1)}\right|=\lim_(n\to\infty)\left|((1*3*5*\cdots*(2n-1)*(2n+1))/((2n+1)!))/((1*3*5*\cdots*(2n-1))/((2n-1)!))\right|`

`\displaystyle=\lim_(n\to\infty)\left|((2n+1)/((2n+1)(2n)))/(\frac11)\right|=\lim_(n\to\infty)\frac1{2n}=0<1`

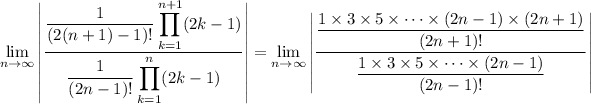
Since
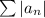
`\sum|a_n|` converges by the ratio test, the series
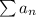
`\sum a_n` converges absolutely.