Find the x-coordinate of the point on the graph of y=x^2 where the tangent line is parallel to the secant line that cuts the curve at x=-1 and x=2 Please how do you solve this?<…

Question

asked Nov 13, 2018 93.3k views

1 Answer

Ingalcala · Answer 1 · 2018-11-19T10:41:20+0000

First find the secant line. The slope of the secant line through
(-1,1)

(when

) and

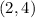
(when

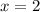
) is the average rate of change of
y=x^2

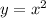
over the interval
[-1,2]

:

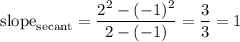
$\text{slope}_{\text{secant}}=(2^2-(-1)^2)/(2-(-1))=\frac33=1$

The tangent line to
y=x^2

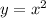
will have a slope determined by the derivative:

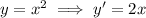
$y=x^2\implies y'=2x$

Both the secant and tangent will have the same slope when
2x=1

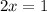
, or when
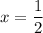
$x=\frac12$ .