Question

Find the period of a pendulum that has a length of .6m and is on earth. Make sure that you show your work and prominently display the equation that you use to solve it.

Answer 1

The period of this pendulum is
`T=1.55\: s`

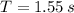
Step-by-step explanation:

The equation of motion of a pendulum is given by:

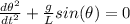`(d\theta^(2))/(dt^(2))+(g)/(L)sin(\theta)=0` (1)

Where:

θ is the angle of motion

g is the gravity at the earth surface (9.81 m/s²)

L is the length of the pendulum (0.6 m)

Now, using equation (1) we can find the square angular frequency (ω), it will be:

`\omega^(2)=(g)/(L)`

`\omega=\sqrt{(g)/(L)}`

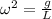
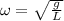
Let's recall that the angular frequency is
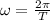`\omega=(2\pi)/(T)`, then the period will be:

`T=(2\pi)/(\omega)`

`T={2\pi}\sqrt{(L)/(g)`

`T=2\pi}\sqrt{(0.6)/(9.81)`

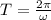
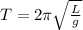
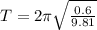
Therefore, the period of this pendulum is
`T=1.55\: s`

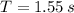
I hope it helps you!