Question

Paul’s bicycle shop, 40 bicycles are inspected. If 20 needed new tires and 30 needed gear repairs, answer the following: a. What is the greatest number of bikes that could have needed both? b. What is the least number of bikes that could have needed both? c. What is the greatest number of bikes that could have needed neither?

Answer 1

A:20 because there was only 20 that needed tires.
B:10 because the difference between 20 and 30 is 10
C:10 because you still have the other bikes that needed repaired

Answer 2

Answer: 1) 20, 2) 10, 3) 10

Explanation:

Since we have given that

Number of bicycles surveyed = 40

Number of people who needed new tires = 20

Number of people who needed gear repairs = 30

a. What is the greatest number of bikes that could have needed both?

Greatest number of bikes that needed both = 20

Suppose 20 people who needed new tires also needed gear repairs.

b. What is the least number of bikes that could have needed both?

Least number of bikes that needed both = 10

Suppose 10 people among 20 needed tires and 10 people among 30 needed gear repairs.

That 10 people needed both.

i.e.

`n(A\cup B)=n)A)+n(B)-n(A\cap B)\\\\40=20+30-n(A\cap B)\\\\40-50=-n(A\cap B)\\\\10=n(A\cap B)`

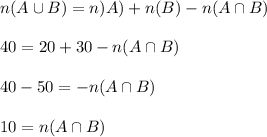
c. What is the greatest number of bikes that could have needed neither?

Let suppose that 20 people among 30 people needed gear repairs and 10 people among 20 people needed new tires.

So, 40-(20+10)=40-30 = 10

10 people are those who could have needed neither.

Hence, 1) 20, 2) 10, 3) 10