Question

Given b = 12, c = 15 and A = 60° in triangle ABC, use the Law of Cosines to solve for a. Fill in the blank(s) to complete each step. If applicable, be sure to enter all decimal numbers with a zero in the ones place. Round your final answer to the nearest hundredth.

Answer 1

a^2 = b^2 + c^2 -2bc * cos(A)
a^2 = 144 + 225 -360 * .5
a^2 = 189
a = 13.748

Answer 2

13.75

Explanation:

We have been given that side b = 12, c = 15 and A = 60° in triangle ABC. We are asked to find the measure of a using law of cosines.

`a^2=b^2+c^2-2bc* \text{cos}(A)`, where, a, b and c are length of sides of triangle and A is opposite angle to side A.

Upon substituting our given values in above formula we will get,

`a^2=12^2+15^2-2*12*15* \text{cos}(60^(\circ))`

`a^2=144+225-360* \text{cos}(60^(\circ))`

`a^2=369-360* 0.5`

`a^2=369-180`

`a^2=189`

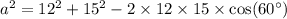
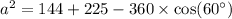
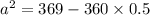
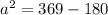
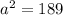
Now, we will take square root of both sides of our given equation.

`a=√(189)`

`a=13.74772708486752\approx 13.75`

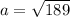
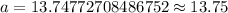
Therefore, the length of a is 13.75.