Question

Please help asap, thank you!

Answer 1

x ≈ 2.1

y ≈ 5.4

w = 5

Explanation:

The given parameters are;

Segment AC = 13

Segment BC = y

Segment AD = 12

Segment CD = w

Segment BD = x

By Pythagoras's theorem, for the right triangle ΔACD, we have;

`\overline {AC}`² =
`\overline {AD}`² +
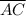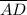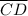`\overline {CD}`²

∴ 13² = 12² + w²

w² = 13² - 12² = 25

w = √(25) = 5

w = 5

By, Pythagoras's theorem similarly, in the right triangle ΔBCD we have;

y² = x² + w²

∴ y² = x² + 5² = x² + 25

y² = x² + 25

In the right triangle ΔABC we have;

`\overline {AB}`² =
`\overline {AC}`² +
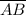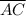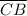`\overline {CB}`²

∴ (12 + x)² = 13² + y² = 13² + (x² + 25)

(12 + x)² = 13² + (x² + 25)

144 + 24·x + x² = 13² + x² + 25

24·x = 13² + 25 - 144 = 50

x = 50/24 ≈ 2.1

x ≈ 2.1

y² = x² + 25

∴ y = √(x² + 25) = √((50/24)² + 25) = 65/12 ≈ 5.4

y ≈ 5.4