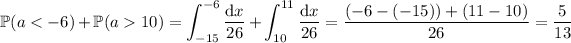Question

General Continuous Random Variable problem. Given a is uniformly distributed over [-15,11], what is the probability that the roots of the equation are both real?

Answer 1

The roots are both real when the discriminant of the quadratic is positive:


`a^2-4(a+15)=a^2-4a-60=(a-10)(a+6)>0`

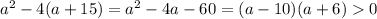
When
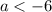
`a<-6`, say
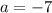
`a=-7`, you have
`(-7-10)(-7+6)=17>0`.
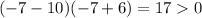
When
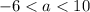
`-6<a<10`, say
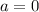
`a=0`, you have
`(0-10)(0+6)=-60<0`.
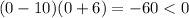
When
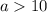
`a>10`, say
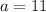
`a=11`, you have
`(11-10)(11+6)=17>0`.

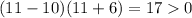
So the quadratic will have two real roots whenever
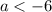
`a<-6` or
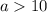
`a>10`. The probability of this occurring is


`\mathbb P((a<-6)\lor(a>10))=\mathbb P(a<-6)+\mathbb P(a>10)`

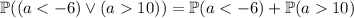
The density function for this random variable is


`f_X(x)=\begin{cases}\frac1{11-(-15)}=\frac1{26}&\text{for }-15\le x\le11\\\\0&\text{otherwise}\end{cases}`

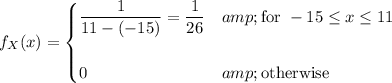
so


`\mathbb P(a<-6)+\mathbb P(a>10)=\displaystyle\int_(-15)^(-6)(\mathrm dx)/(26)+\int_(10)^(11)(\mathrm dx)/(26)=((-6-(-15))+(11-10))/(26)=\frac5{13}`