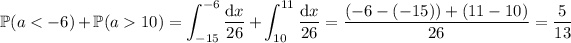The roots are both real when the discriminant of the quadratic is positive:
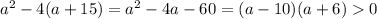
When
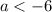
, say
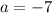
, you have

.
When
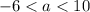
, say
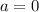
, you have
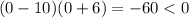
.
When

, say
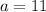
, you have

.
So the quadratic will have two real roots whenever
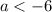
or

. The probability of this occurring is
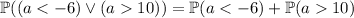
The density function for this random variable is
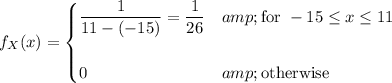
so