The equation
We must find the equation that models the amount of medication in the bloodstream as a function of the days passed from the initial dose. The initial dose is a and we are going to use x for the number of days and M for the amount of mediaction in the bloodstream. We are going to model this using an exponential function which means that the variable x must be in the exponent of a power:

We are told that the half-life of the medication is 6 hours. This means that after 6 hours the amount of medication in the bloodstream is reduced to a half. If the initial dose was a then the amount after 6 hours has to be a/2. We are going to use this to find the parameter b but first we must convert 6 hours into days since our equation works with days.
Remember that a day is composed of 24 hours so 6 hours is equivalent to 6/24=1/4 day. This means that the amount of medication after 1/4 days is the half of the initial dose. In mathematical terms this means M(1/4)=M(0)/2:
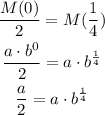
We can divide both sides of this equation by a:
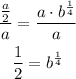
Now let's raised both sides of this equation to 4:
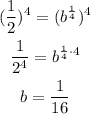
Which can also be written as:

Then the equation that models how much medication will be in the bloodstream after x days is:
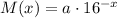
Using this we must find how much medication will be in the bloodstream after 4 days for an initial dose of 500mg. This basically means that a=500mg, x=4 and we have to find M(4):
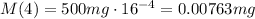
So after 4 days there are 0.00763 mg of medication in the bloodstream.
Now we have to indicate how much more medication will be if the initial dose is 750mg instead of 500mg. So we take a=750mg and x=4:
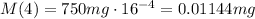
If we substract the first value we found from this one we obtained the required difference:
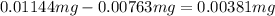
So the answer to the third question is 0.00381mg.