Question

Ed Sloan invests $1,600 at the beginning of each year for eight years into an account that pays 10% compounded semiannually. The value of the annuity due is (use the tables in the handbook):

Answer 1

The answer is: $39,748.80

Explanation:

The principle amount is p = $1600

rate is 10% or 0.10 but as its compounded semiannually it becomes,

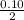`(0.10)/(2)` = 0.05

n =
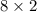`8* 2` =16

Formula is :

`p((1+r)^(n)-1 (1+r))/(r)`

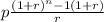
Putting values in formula we get

`(1600(1+0.05)^(16)-1(1+0.05) )/(0.05)`

`(1600(1.05)^(16)-1(1.05) )/(0.05)`

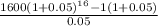
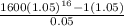
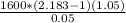`(1600*(2.183-1)(1.05))/(0.05)` = 39748.80

The value of the annuity due is $39,748.80

Answer 2

FV=PV(r+1)ⁿ
FV=Future value, or your amount of money you're going to have after 8 years.
PV=Present value, or the amount of money you have just invested.
APR=10
FV=1,600(10+1)¹⁶
FV=1,600(11)¹⁶
FV=1,600(176)
FV=$281,600