Question

Growth Models 19515. In 1968, the U.S. minimum wage was $1.60 per hour. In 1976, the minimum wagewas $2.30 per hour. Assume the minimum wage grows according to an exponentialmodel where n represents the time in years after 1960.a. Find an explicit formula for the minimum wage.b. What does the model predict for the minimum wage in 1960?c. If the minimum wage was $5.15 in 1996, is this above, below or equal to whatthe model predicts?

Answer 1

In general, the exponential growth function is given by the formula below

`f(x)=a(1+r)^x`

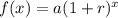
Where a and r are constants, and x is the number of time intervals.

In our case, n=0 for 1960; therefore, 1968 is n=8,

`\begin{gathered} f(8)=a(1+r)^8 \\ \text{and} \\ f(8)=1.6 \\ \Rightarrow1.6=a(1+r)^8 \end{gathered}`

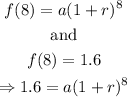
And 1976 is n=16

`\begin{gathered} f(16)=a(1+r)^(16) \\ \text{and} \\ f(16)=2.3 \\ \Rightarrow2.3=a(1+r)^(16) \end{gathered}`

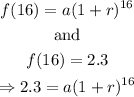
Solve the two equations simultaneously, as shown below

`\begin{gathered} (1.6)/((1+r)^8)=a \\ \Rightarrow2.3=(1.6)/((1+r)^8)(1+r)^(16) \\ \Rightarrow2.3=1.6(1+r)^8 \\ \Rightarrow(2.3)/(1.6)=(1+r)^8 \\ \Rightarrow((2.3)/(1.6))^{(1)/(8)}=(1+r)^{}^{} \\ \Rightarrow r=((2.3)/(1.6))^{(1)/(8)}-1 \\ \Rightarrow r=0.0464078 \end{gathered}`

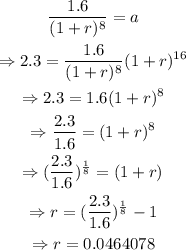
Solving for a,

`\begin{gathered} r=0.0464078 \\ \Rightarrow a=(1.6)/((1+0.0464078)^8)=1.113043\ldots \end{gathered}`

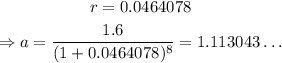
a) Thus, the equation is

`\Rightarrow f(n)=1.113043\ldots(1+0.0464078\ldots)^n`

b) 1960 is n=0; thus,

`f(0)=1.113043\ldots(1+0.0464078\ldots)^0=1.113043\ldots`

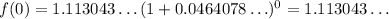
The answer to part b) is $1.113043... per hour

c)1996 is n=36

`\begin{gathered} f(36)=1.113043\ldots(1+0.0464078\ldots)^(36) \\ \Rightarrow f(36)=5.6983\ldots \end{gathered}`

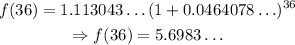
The model prediction is above $5.15 by $0.55 approximately. The answer is 'below'