We are asked to determine the x-coordinate of the center of mass of the given bricks. To do that, we will use the following formula:
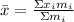
Where:

Since we have three bricks, the formula expands to:
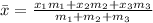
Since we have three bricks with the same characteristics we will assume the three of them have the same mass:
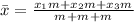
Taking "m" as a common factor and adding like terms in the denominator we get:
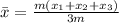
Now we cancel out the "m":
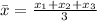
Now we determine the x-coordinates of each brick. Each brick is a parallelepiped, therefore, the x-coordinate is in the middle. Since each brick measures L, this means that the x-coordinate of the first brick is:
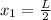
For the second brick, we have the L/2 of the separation from the first plus the L/2 of its length, therefore:
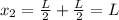
Now, for the third brick we have the L/4 of the separation from the second brick plus the L/2 of the separation of the second brick and the first brick and the L/2 of the length of the third brick, therefore:
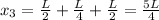
Now we substitute in the formula for the x-coordinate:

Adding like terms in the numerator:

Simplifying:
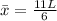
Therefore, the x-coordinate of the center of mass is located at 11L/6 from the origin.