Question

44) Find the x coordinate of the center of mass of the bricks shown.

Answer 1

The x-coordinate of the center of mass for the three bricks, each of length L, is
`\( (11L)/(12) \)`.

To determine the x-coordinate of the center of mass (COM) for the three bricks, each of length L, laid on the x-axis, we need to consider the distribution of mass along the axis. Let's denote the position of the center of mass of each brick.

1. The center of mass of the first brick, placed at the origin (x = 0), is at x = L/2.

2. For the second brick, which is positioned L/2 away from the first, its center of mass is at (L/2 + L/2) = L.

3. The third brick is L/4 away from the second brick. The center of mass of the third brick contributes to the COM at (L + L/4) = 5L/4.

Now, we find the overall center of mass (COM) by calculating the weighted average of these positions:

`\[ \text{COM} = (m_1 \cdot x_1 + m_2 \cdot x_2 + m_3 \cdot x_3)/(m_1 + m_2 + m_3) \]`

Since the masses of the bricks are the same, the expression simplifies to:

`\[ \text{COM} = (L/2 + L + 5L/4)/(3) = (11L/4)/(3) = (11L)/(12) \]`

Therefore, the x-coordinate of the center of mass of the three bricks is
`\( (11L)/(12) \)`.

Answer 2

We are asked to determine the x-coordinate of the center of mass of the given bricks. To do that, we will use the following formula:

`\bar{x}=(\Sigma x_im_i)/(\Sigma m_i)`

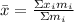
Where:

`\begin{gathered} x_i=\text{ x-coordinate of the center of mass of each brick} \\ m_i=\text{ mass of each brick} \end{gathered}`

Since we have three bricks, the formula expands to:

`\bar{x}=\frac{x_1m_1+x_2m_2_{}+x_3m_3}{m_1+m_2+m_3}`

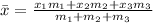
Since we have three bricks with the same characteristics we will assume the three of them have the same mass:

`\bar{x}=\frac{x_1m_{}+x_2m+x_3m_{}}{m_{}+m_{}+m_{}}`

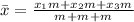
Taking "m" as a common factor and adding like terms in the denominator we get:

`\bar{x}=(m(x_1+x_2+x_3))/(3m)`

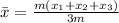
Now we cancel out the "m":

`\bar{x}=(x_1+x_2+x_3)/(3)`

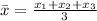
Now we determine the x-coordinates of each brick. Each brick is a parallelepiped, therefore, the x-coordinate is in the middle. Since each brick measures L, this means that the x-coordinate of the first brick is:

`x_1=(L)/(2)`

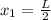
For the second brick, we have the L/2 of the separation from the first plus the L/2 of its length, therefore:

`x_2=(L)/(2)+(L)/(2)=L`

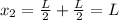
Now, for the third brick we have the L/4 of the separation from the second brick plus the L/2 of the separation of the second brick and the first brick and the L/2 of the length of the third brick, therefore:

`x_3=(L)/(2)+(L)/(4)+(L)/(2)=(5L)/(4)`

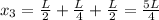
Now we substitute in the formula for the x-coordinate:

`\bar{x}=(((L)/(2))+(L)+((5L)/(4)))/(3)`

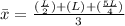
Adding like terms in the numerator:

`\bar{x}=((11L)/(2))/(3)`

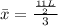
Simplifying:

`\bar{x}=(11L)/(6)`

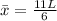
Therefore, the x-coordinate of the center of mass is located at 11L/6 from the origin.