Question

Suppose that $16,065 is invested at an interest rate of 6.6% per year, compounded continuously. a) Find the exponential function that describes the amount in the account after time t, in years. b) What is the balance after 1 year? 2 years?5 years? 10 years? c) What is the doubling time?

Answer 1

Okay, here we have this:

Considering the provided information we obtain the following:

a)

Replacing in the Compound Interest formula we obtain the following:

`\begin{gathered} A(t)=Pe^(rt) \\ A(t)=16065e^(0.066t) \end{gathered}`

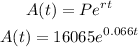
b)

After 1 year (t=1):

`\begin{gathered} A(1)=16065e^(0.066(1)) \\ A(1)\approx17,161.06 \end{gathered}`

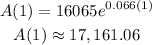
We obtain that after one year the balance is aproximately $17,161.06.

After 2 years (t=2):

`\begin{gathered} A(2)=16065e^(0.066(2)) \\ A(2)=18331.90 \end{gathered}`

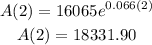
We obtain that after two years the balance is aproximately $18,331.90

After 5 years (t=5):

`\begin{gathered} A(5)=16065e^(0.066(5)) \\ A(5)=$22,345.90$ \end{gathered}`

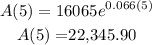
We obtain that after five years the balance is aproximately $22,345.90.

After 10 years (t=10):

`\begin{gathered} A(10)=16065e^(0.066(10)) \\ A(10)=$31,082.44$ \end{gathered}`

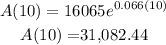
We obtain that after ten years the balance is aproximately $31,082.44.

c)

In this case the doubling time will be when she has double what she initially had, that is: $16,065*2=$32130, replacing in the formula:

`32130=16065e^(0.066t)`

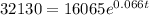
Let's solve for t:

`\begin{gathered} 32130=16065e^(0.066t) \\ 16065e^{\mleft\{0.066t\mright\}}=32130 \\ (16065e^(0.066t))/(16065)=(32130)/(16065) \\ e^{\mleft\{0.066t\mright\}}=2 \\ 0.066t=\ln \mleft(2\mright) \\ t=(\ln\left(2\right))/(0.066) \\ t\approx10.502years \end{gathered}`

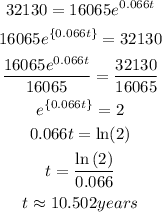
Finally we obtain that the doubling time is approximately 10.502 years or about 10 years 6 months.