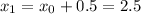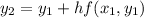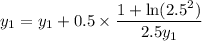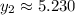Question

Using Euler’s Method with a step size of h=0.5, estimate the value for y(3) for the differential equation xy dy/dx= 1+ln(x^2), with y(2)=5.

a. 5.352

b. 5.230

c. 5.238

d. 5.233

Answer 1

Euler's method uses the recurrence relation


`y_(n+1)=y_n+hf(x_n,y_n)`

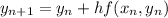
to approximate the value of the solution
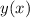
`y(x)` to the ODE
`y'=f(x,y)`.


`xy(\mathrm dy)/(\mathrm dx)=1+\ln(x^2)\implies y'=(1+\ln(x^2))/(xy)=f(x,y)`

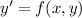
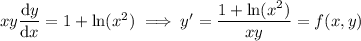
With a step size of
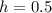
`h=0.5`, there will only be two steps necessary to find the approximate value of
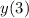
`y(3)` based on the initial point
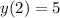
`y(2)=5`. See the attached table below for the computation results.

To demonstrate how the table is generated: Since
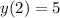
`y(2)=5`, you are using
`(x_0,y_0)=(2,5)`.


`y_1=y_0+hf(x_0,y_0)`

`y_1=5+0.5*(1+\ln(2^2))/(2*5)`

`y_1\approx5.1193`

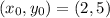
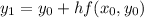
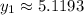
The next point then uses
`x_1=x_0+0.5=2.5`


`y_2=y_1+hf(x_1,y_1)`

`y_1=y_1+0.5*(1+\ln(2.5^2))/(2.5y_1)`

`y_2\approx5.230`