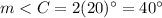Question

The measures of the angles of △ABC are given by the expressions in the table. Angle Measure A 48° B (6x−28)° C (2x)° Find the value of x. Then find the measures of angles B and C. Enter your answers in the boxes. x = ​ m∠B= ​ 48 º ​ m∠C= ​ 12 º

Answer 1

A 48°

B (6x−28)°

C (2x)°

48 + 6x -28 + 2x = 180 degrees

8x = 160 degrees

x = 20

angle B = 6x - 28 = 92

angle C = 2x = 40

Double-Check

Angle A + B + C = 48 + 92 + 40

Angle A + B + C = 180 degrees

Answer 2

Part 1) the value of x is
`20\°`

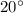
Part 2)
`m<B=92\°`

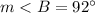
Part 3)
`m<C=40\°`

Explanation:

Part 1)

Find the value of x

we know that

The sum of the internal angles of a triangle must be equal to
`180\°`

so

In this problem

`m<A+m<B+m<C=180\°`

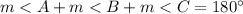
substitute the values

`48\°+(6x-28)\°+(2x)\°=180\°`

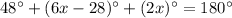
solve for x

`8x+20\°=180\°`

`8x=180\°-20\°`

`x=160\°/8=20\°`

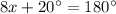
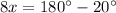
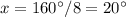
Part 2) Find the measure of angle B

`m<B=(6x-28)\°`

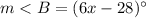
substitute the value of x

`m<B=(6(20)-28)\°=92\°`

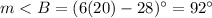
Part 3) Find the measure of angle C

`m<C=(2x)\°`

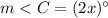
substitute the value of x

`m<C=2(20)\°=40\°`