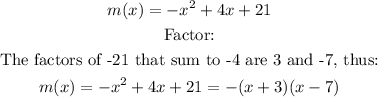
The zeros of the function are:
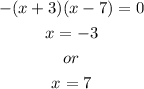
The vertex is a point V(h,k) on the function. It's either at the base or the top of the function, depending upon wether it opens, upward or downward respectively.
For a function of the form:
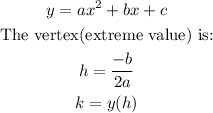
Therefore:
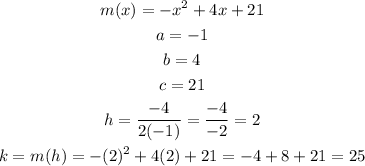
Hence, the extreme value is 25 at x = 2
That's it, do you have any question?