Question

M(x)=-x^2+4x+21. prove the zeros and determine the extreme value algebraically

Answer 1

`\begin{gathered} m(x)=-x^2+4x+21 \\ \text{Factor:} \\ \text{The factors of -21 that sum to -4 are 3 and -7, thus:} \\ m(x)=-x^2+4x+21=-(x+3)(x-7) \end{gathered}`

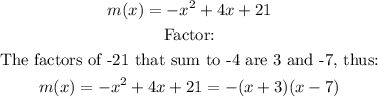
The zeros of the function are:

`\begin{gathered} -(x+3)(x-7)=0 \\ x=-3 \\ or \\ x=7 \end{gathered}`

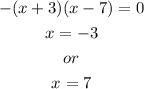
The vertex is a point V(h,k) on the function. It's either at the base or the top of the function, depending upon wether it opens, upward or downward respectively.

For a function of the form:

`\begin{gathered} y=ax^2+bx+c \\ \text{The vertex(extreme value) is:} \\ h=(-b)/(2a) \\ k=y(h) \end{gathered}`

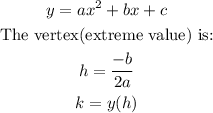
Therefore:

`\begin{gathered} m(x)=-x^2+4x+21 \\ a=-1 \\ b=4 \\ c=21 \\ h=(-4)/(2(-1))=(-4)/(-2)=2 \\ k=m(h)=-(2)^2+4(2)+21=-4+8+21=25 \end{gathered}`

Hence, the extreme value is 25 at x = 2

That's it, do you have any question?