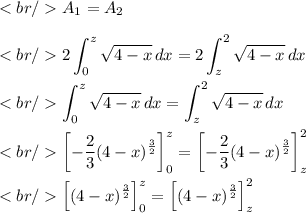Question

Find the value of z such that the line x=z divides the region bounded by the graphs of the equations into 2 regions of equal area.

y²=4-x, x=0 is one bound
the right bound is x=2

show all work and reasoning why you did it
use integrals

Answer 1

We'll put y in function of x:


`image`

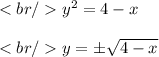
Look the graph of the function in the attached figure. The areas above and below the x-axis are equal. So, we can represent the area bounded by the graph as:


`A=2\displaystyle\int √(4-x)\,dx}`

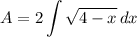
Using that to calculate the area bounded is equal to calculate the double of area above the x-axis.

The line x=z divides the region into two regions of equal area with 0 ≤ x ≤ 2, then:


`image`


`image`