Question

A rumor spreads through a school according to the differential equation dy/dt= 3y(0.5-y). What percentage of the school has heard the rumor when it is spreading the fastest?

a.75
b.50
c.25

Answer 1

`\bf \cfrac{dy}{dt}=3y(0.5-y)\to 1.5y-3y^2`

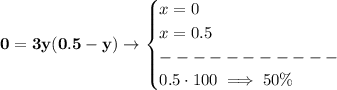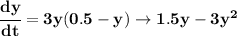
so.. notice, the derivative is a quadratic with a negative coefficient
on the leading term,
that means, is a parabola opening downwards, it only has one
extrema, a maximum point, at its vertex,

what's the derivative at the vertex? well, is a horizontal tangent line,
thus, slope is 0, so, if you set the derivative to 0, you'll get the
maximum point, or, the peak of the rate for the rumor,

so, what the dickens is "y" at that point?
well

`\bf 0=3y(0.5-y)\to \begin{cases} x=0\\ x=0.5\\ -----------\\ 0.5\cdot 100\implies 50\% \end{cases}`