Question

A genetic experiment involving peas yielded one sample of offspring consisting of 409 green peas and 171 yellow peas. Use a 0.05 significance level to test the claim that under the same​ circumstances, 26​% of offspring peas will be yellow. Identify the null​ hypothesis, alternative​ hypothesis, test​ statistic, P-value, conclusion about the null​ hypothesis, and final conclusion that addresses the original claim. Use the​ P-value method and the normal distribution as an approximation to the binomial distribution.

Answer 1

The usual expectation for this kind of experiment is that the peas would yield green and yellow peas in a 3:1 ratio, or 75% green to 25% yellow. So your null hypothesis is that the proportion of yellow peas is
`p=0.25`.

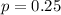
You're testing the claim that 26% of the offspring will be yellow, which means the alternative hypothesis is that the proportion of yellow peas is actually 0.26, or more generally that the expected proportion is greater than 0.25, or
`p>0.25`.

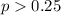
The test statistic in this case will be


`Z=\frac{\hat p-p_0}{\sqrt{\frac{p_0(1-p_0)}n}}`

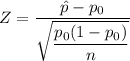
where
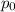
`p_0` is the proportion assumed under the null hypothesis,
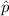
`\hat p` is the measured proportion, and
`n` is the sample size. You have
`p_0=0.25`,
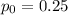
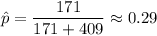
`\hat p=(171)/(171+409)\approx0.29`, and
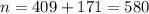
`n=409+171=580`, so the test statistic is


`Z=\frac{0.29-0.25}{\sqrt{(0.25*0.75)/(580)}}\approx2.2247`

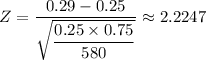
Because you're testing
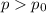
`p>p_0`, this is a right-tailed test, so the P-value is


`\mathbb P(Z>2.2247)\approx0.0131`

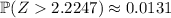
The critical value for a right-tail test at a 0.05 significance level is
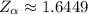
`Z_\alpha\approx1.6449`, which means the rejection region is any test statistic that is larger than this critical value. Since
`Z>Z_\alpha` in this case, we reject the null hypothesis.

So the conclusion for this test is that the sample proportion is indeed statistically significantly different from the proportion suggested by the null hypothesis.

Answer 2

Explanation:

Given that observed green peas are 409 and 171 yellow peas.

Create hypotheses as:

H0: 26% are yellow and 74% are green

Ha: yellow and green are not as above

(Two tailed chi square test)

Let us calculate expected yellow and green

Total peas = 580: out of this 26% yellow i.e. 150.8

and green peas are 429.2

Observed o 409 171

Expected e 429.2 150.8

Chi square 0.951 2.706 3.657

=
`((o-e)^2)/(e)`

Chisquare statistic = 3.657 and df = 1

p value for 95% =0.056>0.05

AT 5% significance level, we accept null hypothesis

26% of off spring are yellow can be accepted