Question

You roll a six-sided die twice. What is the probability of rolling an even number and then an odd number?A)1B)1/3 큼C)nilaD)

Answer 1

Let's begin by listing out the given information:

A fair dice has 6 sides

The dice has its sides numbered from 1-6

The number of sides with even numbers (2, 4 & 6) equals 3

The number of sides with odd numbers (1, 3 & 5) equals 3

The probability of rolling an even number is given as shown below:

`\begin{gathered} P=\frac{Number\text{ of Possible Outcome}}{Total\text{ Number of Outcome}} \\ P\mleft(even\mright)=(3)/(6)=(1)/(2) \\ P(even)=(1)/(2) \end{gathered}`

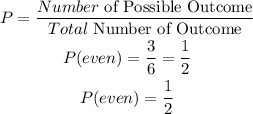
The probability of rolling an odd number is given as shown below:

`\begin{gathered} P=\frac{Number\text{ of Possible Outcome}}{Total\text{ Number of Outcome}} \\ P(odd)=(3)/(6)=(1)/(2) \\ P(odd)=(1)/(2) \end{gathered}`

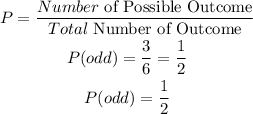
The probability of rolling an even number followed by an odd number is obtained by the product of the probabilities above. We have:

`\begin{gathered} P(even,odd)=P(even)* P(odd) \\ P(even,odd)=(1)/(2)*(1)/(2)=(1)/(4) \\ P(even,odd)=(1)/(4) \end{gathered}`

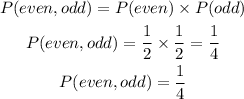
Therefore, the probability of rolling an even number and then an odd number is 1/4