Question

Sun, a kayaker, paddles 8 miles upstream (against the current) in 2 hours. Returning to her original location, she paddles downstream (with the current) the same distance in 1 hour. The equations represent x, the paddling speed, and y, the speed of the current.2(x – y) = a

b(x + y) = 8

Which are true? Check all that apply.

a = 8


b = 8


a = 1


b = 1


a = b

Answer 1

A d

Explanation:

Answer 2

a=8 and b=1

Explanation:

Given : Sun, a kayaker, paddles 8 miles upstream (against the current) in 2 hours. Returning to her original location, she paddles downstream (with the current) the same distance in 1 hour. The equations represent x, the paddling speed, and y, the speed of the current.

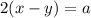`2(x - y) = a` and
`b(x + y) = 8`

To find : Which are true?

Solution :

If x represents the paddling speed, and y represents the speed of the current.

The relative speed in upstream is x-y

Relative time in downstream= x+y

A kayaker, paddles 8 miles upstream (against the current) in 2 hours.

`\text{Distance}=\text{Speed} * \text{Time}`

`8=(x-y)* 2`

Comparing with
`2(x - y) = a`

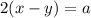
We get, a=8

Returning to her original location, she paddles downstream (with the current) the same distance in 1 hour.

`\text{Distance}=\text{Speed} * \text{Time}`

`8=(x+y)* 1`

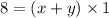
Comparing with
`b(x + y) = 8`

We get, b=1

Thus, a=8 and b=1

Therefore, Option 1 and 4 is correct.