Answer:
The SST for the data set is:
Option: C
C. 26
Explanation:
SST i.e. Sum -Squared Total, is the Total of Sum of the Squares.
SST is calculated as follows:
1) First calculate the mean of the y-value of the given data.
2) Subtract each y-value from the mean calculated above and take the square of the difference quantity.
3) Add or sum these square quantities to obtain SST.
We proceed as follows:
The y-value are:
4 6 11
The mean of these y-values are:
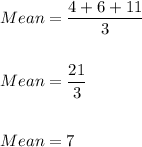
Difference of the data set from mean is:
4-7= -3
6-7= -1
11-7=4
Square of these difference quantity is:
(-3)²=9
(-1)²=1
(4)²=16
Sum of these squared quantity i.e. SST is:
SST=9+1+16
SST=26
Hence, the answer is:
Option: C