Question

Michael's High School is selling tickets to its spring musical. On the first day of ticket sales the school sold 1 adult ticket and 3 student tickets for a total of $38. The second day of sales, the school sold 5 adult tickets and 1 student ticket for a total of $78

Write a system of equations to represent the number of tickets sold each day

Determine the price of an adult ticket and a student ticket

Answer 1

adult ticket price: $14

student ticket price: $8

Explanation:

x = adult ticket

y = student ticket

system equations:

`x + 3y = 38 \\ 5x + y = 78`

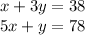
elimination method:
`x + 3y = 38 |multiple \: by \: 1\\ 5x + y = 78|multiple \: by \: 3 \\ \\ x + 3y = 38 \\ 15x + 3y = 234 \\ subract \: them: \\ - 14x = - 196`

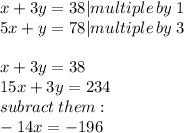
substitute:
`- 14x = - 196 \\ - x = ( - 196)/(14) \\ - x = - 14 \\ x = 14`

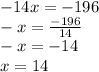
find the y using substitution method:

x+3y=38

14+3y=38

3y=24

y=24/3

y=8

so the price of an adult ticket is $14 and the price of student ticket is $3