Answer
c. Henry's body eliminated the antibiotic at half of the rate at which Greg's body eliminated the antibiotic.
Step-by-step explanation
To solve this, we are using the exponential decay function
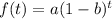
where
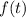 is the final amount remaining after
is the final amount remaining after
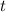 hours
hours
 is the initial amount
is the initial amount
 is the decay rate in decimal form
is the decay rate in decimal form
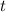 is the time in hours
is the time in hours
We know from our problem that Greg's body is getting rid of the medicine according to the function
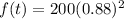 . We can find the decay rate by setting 0.88 equal to 1-b and solve for b:
. We can find the decay rate by setting 0.88 equal to 1-b and solve for b:
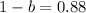
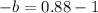
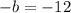

Since the rate is in decimal for, we are going to multiply it by 100% to express it as percentage:
Greg's body rate = 0.12*100% = 12%
Now, to find Henry's body rate, we are using the fact that when
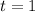 ,
,
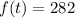 . We can also infer that Henry's initial dose was 300 mg so
. We can also infer that Henry's initial dose was 300 mg so
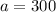 . Let's replace the values in our decay function to find
. Let's replace the values in our decay function to find
 :
:
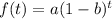
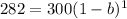
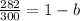
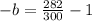

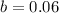
Henry's body rate = 0.06*100% = 6%
Since 6% is half of 12%, Henry's body eliminated the antibiotic at half of the rate at which Greg's body eliminated the antibiotic.