Question

Find the x value for point C such that AC and BC form a 2:3 ratio.

Segment Points
A= (-3,5) B= (3,0)

Answers:

A. 6
B. -0.6
C. 4
D. -2.4

Answer 1

The answer is B.-0.6

Answer 2

B.
`-0.6`

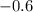
Explanation:

We have been given point C divides A and B such that AC and BC form a 2:3 ratio.

We will use section formula to solve our given problem, which states when a point P internally divides segment AB is ration m:n, then

`[x=(m*x_2+n*x_1)/(m+n),y=(m*y_2+n*y_1)/(m+n)]`

Upon substituting our given values we will get,

`[x=(2*3+3*-3)/(2+3),y=(2*0+3*5)/(2+3)]`

`[x=(6-9)/(5),y=(0+15)/(5)]`

`[x=(-3)/(5),y=(15)/(5)]`

`[x-0.6,y=3]`

Therefore, the value of x is
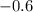`-0.6` and option B is the correct choice.